HW1 -Exercise 3.2: Curve plotting
Although the plot function is designed primarily for plotting standard xy graphs, it can be adapted for other kinds of plotting as well.

1. a)  Make a plot of the so-called deltoid curve, which is defined parametrically by the equations, x = 2 cos θ + cos 2θ, y = 2 sin θ − sin 2θ, where 0 ≤ θ < 2π. Take a set of values of θ between zero and 2π and calculate x and y for each from the equations above, then plot y as a function of x.
2. b)  Taking this approach a step further, one can make a polar plot r = f(θ) for some function f by calculating r for a range of values of θ and then converting r and θ to Cartesian coordinates using the standard equations x = r cos θ, y = r sin θ. Use this method to make a plot of the Galilean spiral, r=θ² for 0 ≤ θ ≤ 10π.
3. c)  Using the same method, make a polar plot of “Fey’s function” in the range 0 ≤ θ ≤ 24π.

Put all 3 plots in one figure with labels making it clear which plot is which.

HW2 – Exercise 5.3:
Consider the integral

a) Write a program to calculate E(x) for values of x from 0 to 3 in steps of 0.1. Choose for yourself what method you will use for performing the integral and a suitable number of slices.
b) When you are convinced your program is working, extend it further to make a graph of E(x) as a function of x.
Note that there is no known way to perform this particular integral analytically, so numerical approaches are the only way forward.

HW3 – Exercise 5.21: Electric field of a charge distribution
Suppose we have a distribution of charges and we want to calculate the resulting electric field. One way to do this is to first calculate the electric potential φ and then take its gradient. For a point charge q at the origin, the electric potential at a distance r from the origin is and the electric field is E = −∇φ.
a) You have two charges, of ±1 C, 10 cm apart. Calculate the resulting electric potential on a 1 m × 1 m square plane surrounding the charges and passing through them. Calculate the potential at 1 cm spaced points in a grid and make a visualization on the screen of the potential using a density plot.
b) Now calculate the partial derivatives of the potential with respect to x and y and hence find the electric field in the xy plane. Make a visualization of the field also. This is a little trickier than visualizing the potential, because the electric field has both magnitude and direction. The matplotlib functions quiver() or streamplot() may be useful here.

HW4 – Exercise 6.16: The Lagrange Point
There is a magical point between the Earth and the Moon, called the L₁ Lagrange point, at which a satellite will orbit the Earth in perfect synchrony with the Moon, staying always in between the two. This works because the inward pull of the Earth and the outward pull of the Moon combine to create exactly the needed centripetal force that keeps the satellite in its orbit. Here’s the setup:

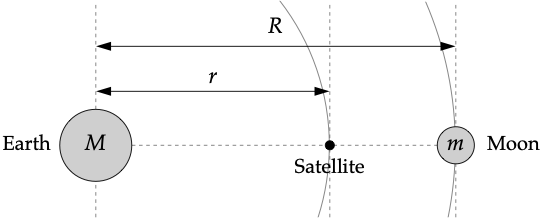
Assuming circular orbits, and assuming that the Earth is much more massive than either the Moon or the satellite, show that the distance r from the center of the Earth to the L₁ point satisfies

where M and m are the Earth and Moon masses, G is Newton’s gravitational constant, and ω is the angular velocity of both the Moon and the satellite.
The equation above is a fifth-order polynomial equation in r (also called a quintic equation). Such equations cannot be solved exactly in closed form, but it’s straightforward to solve them numerically. Write a program that uses either Newton’s method or the secant method to solve for the distance r from the Earth to the L₁ point. Compute a solution accurate to at least four significant figures.
The values G and the Earth’s mass can be found in the astropy.constants or scipy.constants sub-packages. The Moon’s mass is 7.348e22 kg and the Eart-Moon distance is 3.844e8 m. The value of ω is 2.662e-6 s^-1. You will also need to choose a suitable starting value for r, or two starting values if you use the secant method.

HW5 – Exercises 7.4 and 7.6: Fourier filtering and smoothing/ Comparison of DFT and DCT
In the on-line resources you’ll find a file called dow.txt. It contains the daily closing value for each business day from late 2006 until the end of 2010 of the Dow Jones Industrial Average, which is a measure of average prices on the US stock market. Write a program to do the following:
a) Read in the data from dow.txt and plot them on a graph.
b) Calculate the coefficients of the discrete Fourier transform of the data using the function rfft from numpy.fft, which produces an array of N/2 + 1 complex numbers.
c) Now set all but the first 10% of the elements of this array to zero (i.e., set the last 90% to zero but keep the values of the first 10%).
d) Calculate the inverse Fourier transform of the resulting array, zeros and all, using the function irfft, and plot it on the same graph as the original data. You may need to vary the colors of the two curves to make sure they both show up on the graph. Comment on what you see. What is happening when you set the Fourier coefficients to zero?
e) Modify your program so that it sets all but the first 2% of the coefficients to zero and run it again.
Exercise 7.4 looked at data representing the variation of the Dow Jones Industrial Average, colloquially called “the Dow,” over time. The particular time period studied in that exercise was special in one sense: the value of the Dow at the end of the period was almost the same as at the start, so the function was, roughly speaking, periodic. In the on-line resources there is another file called dow2.txt, which also contains data on the Dow but for a different time period, from 2004 until 2008. Over this period the value changed considerably from a starting level around 9000 to a final level around 14000.
a) Write a program similar to the one for Exercise 7.4, part (e), in which you read the data in the file dow2.txt and plot it on a graph. Then smooth the data by calculating its Fourier transform, setting all but the first 2% of the coefficients to zero, and inverting the transform again, plotting the result on the same graph as the original data. As in Exercise 7.4 you should see that the data are smoothed, but now there will be an additional artifact. At the beginning and end of the plot you should see large deviations away from the true smoothed function. These occur because the function is required to be periodic—its last value must be the same as its first—so it needs to deviate substantially from the correct value to make the two ends of the function meet. In some situations (including this one) this behavior is unsatisfactory. If we want to use the Fourier transform for smoothing, we would certainly prefer that it not introduce artifacts of this kind.
b) Modify your program to repeat the same analysis using discrete cosine transforms. You can use the functions from dcst.py to perform the transforms if you wish. Again discard all but the first 2% of the coefficients, invert the transform, and plot the result. You should see a significant improvement, with less distortion of the function at the ends of the inter- val. This occurs because, as discussed at the end of Section 7.3, the cosine transform does not force the value of the function to be the same at both ends.
For this exercise let us use argparse to pass arguments to your code from the command line. Write your code so it can be run on dow.txt or dow2.txt, keep the first 10% or 2% of Fourier coefficients and use DFT or DCT.

HW6 – Exercise 10.3: Brownian motion
Brownian motion is the motion of a particle, such as a smoke or dust particle, in a gas, as it is buffeted by random collisions with gas molecules. Make a simple computer simulation of such a particle in two dimensions as follows. The particle is confined to a square grid or lattice L × L squares on a side, so that its position can be represented by two integers i, j = 0 . . . L − 1. It starts in the middle of the grid. On each step of the simulation, choose a random direction—up, down, left, or right—and move the particle one step in that direction. This process is called a random walk. The particle is not allowed to move outside the limits of the lattice—if it tries to do so, choose a new random direction to move in.
Write a program to perform a million steps of this process on a lattice with L = 101 and make an animation on the screen of the position of the particle. (We choose an odd length for the side of the square so that there is one lattice site exactly in the center.) A movie is the best way to visualize your particles random walk. There are many ways to do this. One example of how to make an animation can be found here.

HW7 – Exercise 10.8: Calculate a value for the integral

,

using the importance sampling formula, Eq. (10.42), with w(x) = x^−1/2, as follows.
a) Show that the probability distribution p(x) from which the sample points should be drawn is given by

and derive a transformation formula for generating random numbers between zero and one from this distribution.
b) Using your formula, sample N = 1,000,000 random points and hence evaluate the integral. You should get a value around 0.84.

Exercise 8.7: Trajectory with air resistance Many elementary mechanics problems deal with the physics of objects moving or flying through the air, but they almost always ignore friction and air resistance to make the equations solvable. If we’re using a computer, however, we don’t need solvable equations. Consider, for instance, a spherical cannonball shot from a cannon standing on level ground. The air resistance on a moving sphere is a force in the opposite direction to the motion with magnitude

where R is the sphere’s radius, ρ is the density of air, v is the velocity, and C is the so-called coefficient of drag (a property of the shape of the moving object, in this case a sphere).

1. Starting from Newton’s second law, F = ma, show that the equations of motion for the position (x, y) of the cannonball are

   

   where m is the mass of the cannonball, g is the acceleration due to gravity, and and are the first and second derivatives of x with respect to time.
2. Change these two second-order equations into four first-order equations using the methods you have learned, then write a program that solves the equations for a cannonball of mass 1 kg and radius 8 cm, shot at 30º to the horizontal with initial velocity 100 ms⁻¹. The density of air is ρ = 1.22 kg m⁻³ and the coefficient of drag for a sphere is C = 0.47. Make a plot of the trajectory of the cannonball (i.e., a graph of y as a function of x).
3. When one ignores air resistance, the distance traveled by a projectile does not depend on the mass of the projectile. In real life, however, mass certainly does make a difference. Use your program to estimate the total distance traveled (over horizontal ground) by the cannonball above, and then experiment with the program to determine whether the cannonball travels further if it is heavier or lighter. You could, for instance, plot a series of trajectories for cannonballs of different masses, or you could make a graph of distance traveled as a function of mass. Describe briefly what you discover.

HW 9 – We will not do a homework set on PDEs. If you would like to practice coding some of these methods Exercises 9.8 and 9.9 from the textbook give a good step by step guide on how to code the Crank-Nicolson method and the spectral method. A copy of the exercises can be found here.